Click detection#
In the following echolocation clicks should be extracted from recorded time series. The particular dataset contains Cuvier’s beaked whale data recorded in the Mediterranean Sea using a passive acoustic recorder. The data are available from “Mobysound”
Load data#
A selected time window of 10 s is loaded for inspection.
import numpy as np
import matplotlib.pyplot as plt
import wave, struct
# load some data from wav files
def wavLoad(fname,t1,dt):
wf = wave.open(fname, 'rb')
nframes=wf.getnframes()
nsw=wf.getsampwidth()
fs=wf.getframerate()
nch=wf.getnchannels()
nbuf=int(dt*fs)
wf.setpos(int(t1*fs))
buf=wf.readframes(nbuf)
wf.close()
data = np.array(struct.unpack('{n}h'.format(n=nbuf*nch),buf))
return data,fs,nch
# data from https://www.mobysound.org/odontocetes/Ziphius_Italy-Annotated.zip
# copied to ./Data/
data,fs,nch=wavLoad("./Data/zc06_204a22410-24210.wav",4,10)
tt=np.arange(np.shape(data)[0])/fs
fig = plt.figure("figure.figsize",[15,5])
plt.plot(tt,data)
plt.xlabel("Time [s]");
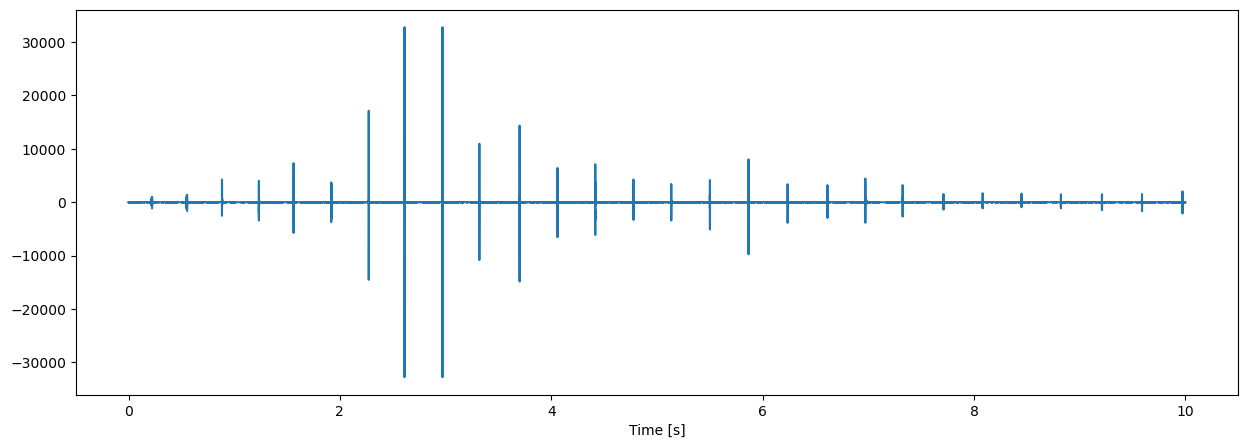
The timeseries shows a typical echolocation click train of odontocetes. Clicks are emitted in a more or less regular fashion. The click amplitude as received by an acoustic recorder are mostly moderate but for short periods of time can become much stronger as evident in above figure.
This phenomenon is typical for echolocation clicks where the animal emits highly focused clicks in forward directions scanning the environment in all possible directions. Whenever the animal is pointing the echolcation sound beam towards the acoustic recorder, the received click amplitude can become strong, but most of the time the animal is searching in other directions and the received click amplitude is much weaker.
Click detection#
Supporting functions#
from numba import jit
@jit(nopython=True,cache=True)
def peak1(xx,leak):
ndat=len(xx)
yy=1.0*xx
for ii in range(1,ndat):
yy[ii]=np.maximum(xx[ii],yy[ii-1]*leak)
return yy
@jit(nopython=True,cache=True)
def pageTest1(zz,th,bb,aa,nt):
ee=0*zz
dd=0*zz
nn=0*zz
sn=0*zz
no=np.sum(zz[:100],0)/100
nn[0]=no
#
sn[0]=zz[0]/nn[0]
#
ndat=len(zz)
it=0
for ii in range(1,ndat):
sn[ii]=zz[ii]/nn[ii-1]
ee[ii]= ee[ii-1]+(sn[ii]-bb)
if (ee[ii]>th):
ee[ii]=th
dd[ii]=1
if ii-it>=nt:
ee[it:ii]=th
dd[it:ii]=1
if (ee[ii]<0):
ee[ii]=0
nn[ii]=nn[ii-1]+aa*(zz[ii]-nn[ii-1])
it=ii
else:
nn[ii]=nn[ii-1]
return dd,nn
Click detections are obtained using first a leaky peak filter followed by a page-test transient detector
yy=peak1(data**2,0.97)
dd,nn=pageTest1(yy,20,6,1e-3,10)
fig = plt.figure("figure.figsize",[15,5])
plt.semilogy(tt,np.sqrt(yy),tt,np.sqrt(nn))
plt.xlabel("Time [s]");
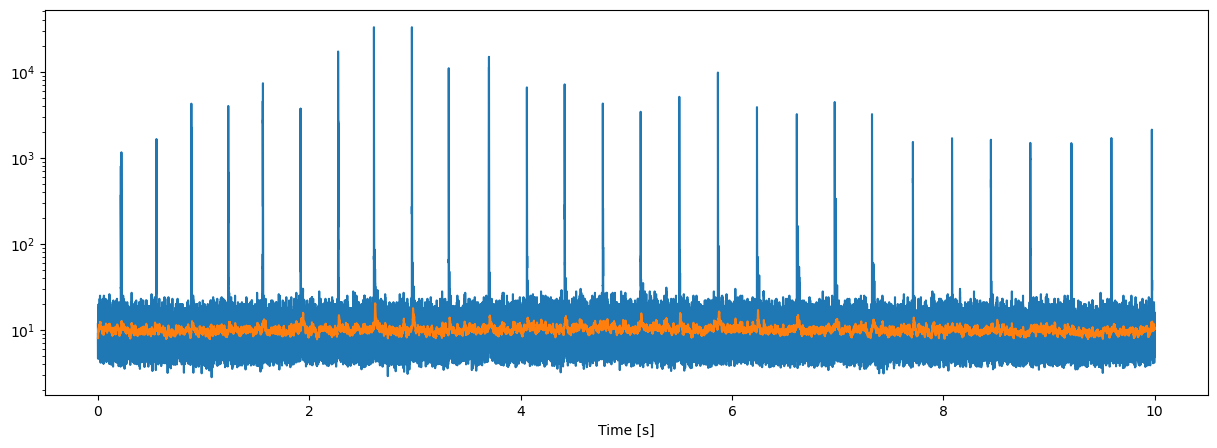
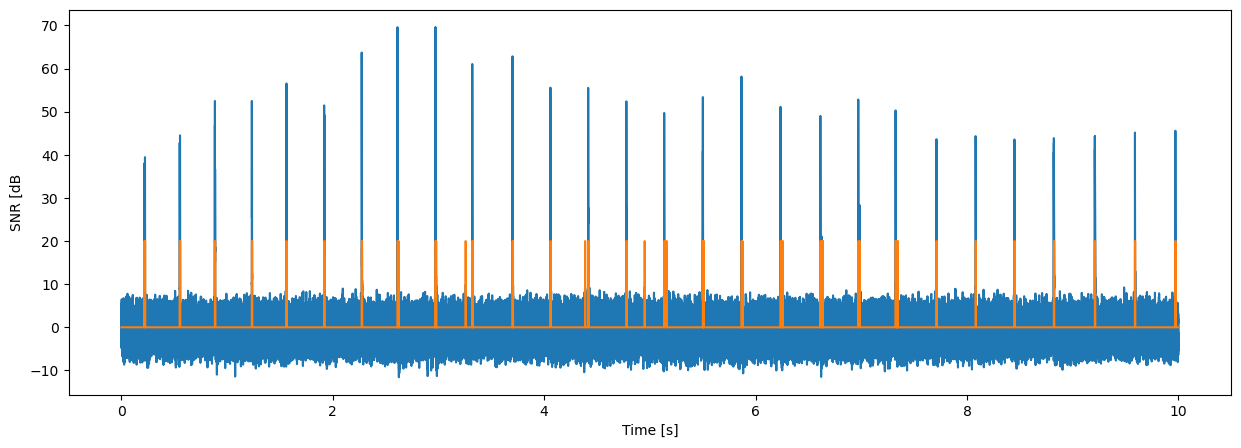
fig = plt.figure("figure.figsize",[15,5])
plt.plot(tt,10*np.log10(yy/nn))
plt.plot(tt,20*dd)
plt.xlabel("Time [s]");
plt.ylabel('SNR [dB');
Load and process beaked whale data#
data,fs,nch=wavLoad("./Data/zc06_204a22410-24210.wav",0, 15)
tt=np.arange(np.shape(data)[0])/fs
yy=peak1(data**2,0.97)
dd,nn=pageTest1(yy,20,6,1e-3,10)
fig = plt.figure("figure.figsize",[15,5])
plt.plot(tt,10*np.log10(yy/nn))
plt.plot(tt,20*dd)
plt.xlabel("Time [s]");
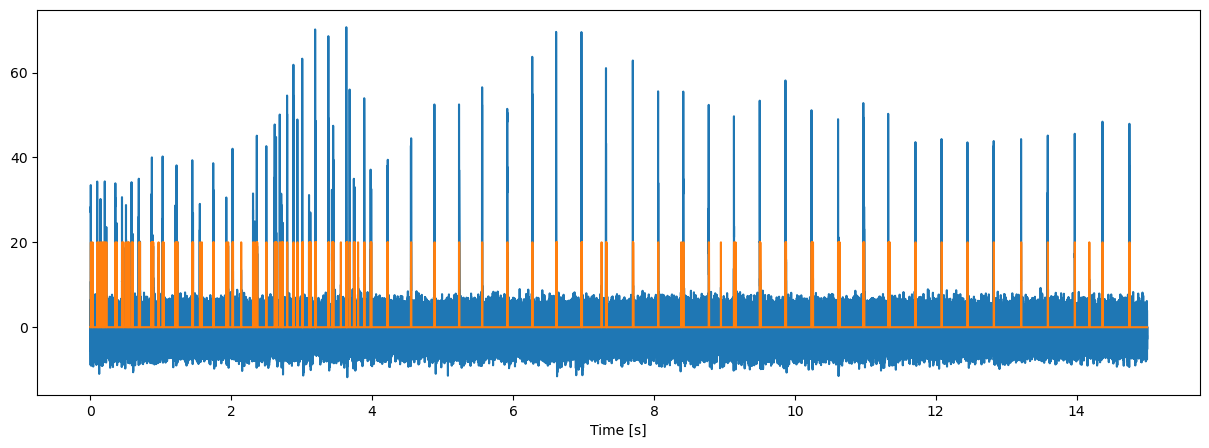
Echolocation click trains are sequences if clicks emitted in a highly correlated fashion, that is, the interval between two consecutive clicks (the Inter-Click_Interval, or ICI) is nearly constant or slowly vaying and to some extend characteristic for the odontocete species.
t1 = np.diff(dd,1,0,prepend=[0])
tcl= tt[t1>0]
ici = np.diff(tcl)
fig = plt.figure("figure.figsize",[15,5])
plt.semilogy(tcl[1:],ici,'.')
plt.xlabel("Time [s]");
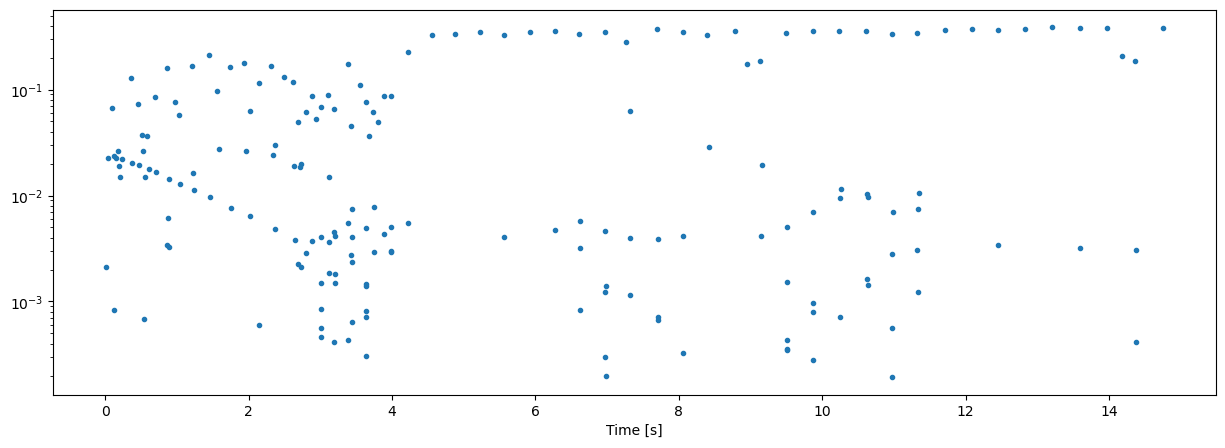
The above plot is an Inter-Detection-Interval (IDI) plot, where all detection are used unlabeled. To obtain the desired ICI, one needs to label these detections properly.
There are three categories of labels
click
boundary reflection of clicks
interfering detections
In case that multiple animals, the interfering detections may be associated with echolocation clicks of another animal.
This is a classical data association problem that can be solved with statistical methods.
Extract clicks and click features#
# search for start and stop of detections
# force start and stop at beginning and end of detections
dd[0]=0
dd[-1]=0
#
id=dd[1:]-dd[:-1]
ip=np.where(id>0)[0] # start of detection
im=np.where(id<0)[0] # stop of detection
det=np.vstack((ip,im))
ndets=np.shape(det)[1]
nc=3
Labels=["TCL","LEN","SNR"]
E=np.zeros((nc,ndets))
E[0,:] = tt[ip]
E[1,:] = det[1,:]-det[0,:] # LEN
for ii in range(ndets):
ix=range(det[0,ii],det[1,ii])
E[2,ii]= np.log10(np.max(yy[ix]/nn[ix])) # SNR
fig = plt.figure("figure.figsize",[15,5])
plt.semilogy(E[0,:],E[1:,:].T,'.');
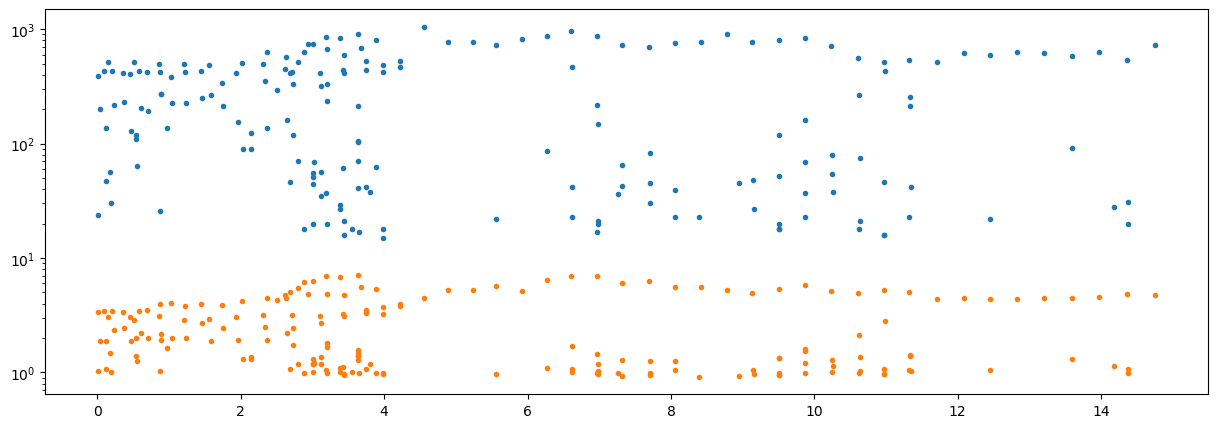
fig = plt.figure("figure.figsize",[15,5])
plt.semilogy(E[1:,:100].T,'.-');
nd=np.shape(E)[1]
n2=1000
A=np.zeros((nd,n2))
for ii in range(nd):
for jj in range(ii+1,nd):
dt=E[0,jj]-E[0,ii]
if dt<1:
kk=int(dt*n2)
if kk<n2:
A[ii,kk]+=1
fig=plt.figure('figure.figsize',[15,10])
im1=plt.imshow(A,origin='lower',cmap=plt.cm.gray_r, aspect='auto')
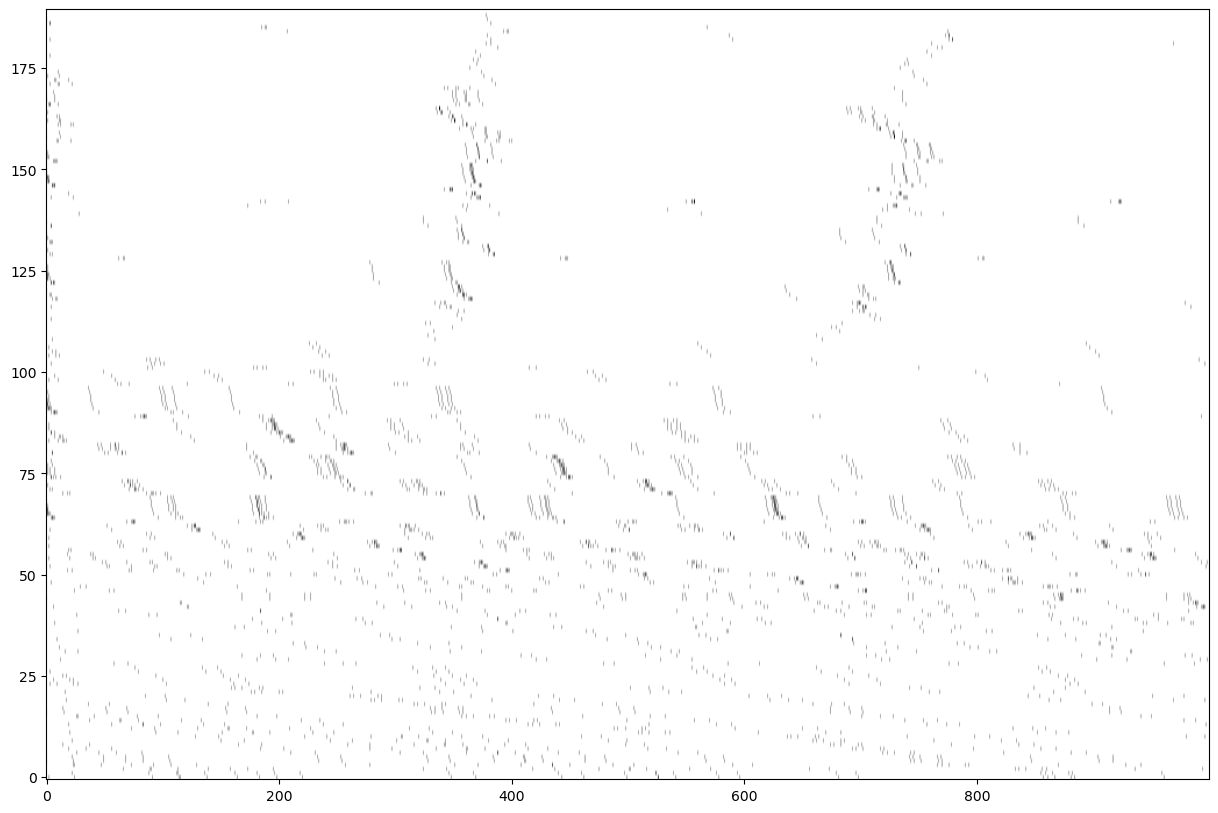
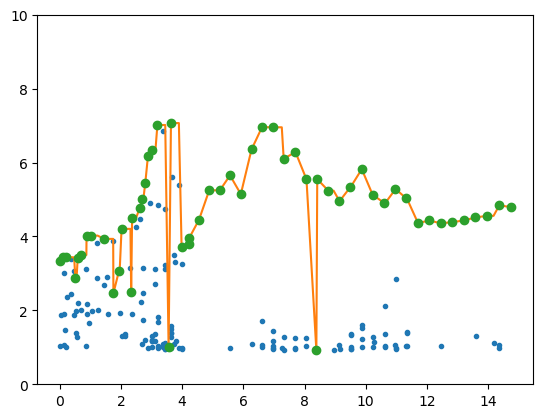
In the following we try to track the strongest SNR peaks assuming that they are a good proxy for clicks.
tcl=E[0,:].T
snr=E[2,:].T
snx=snr.copy()
tcx=tcl.copy()
for ii in range(1,len(snx)):
if (snx[ii]<snx[ii-1]):
if (tcx[ii]-tcx[ii-1]<0.3):
tcx[ii]=tcx[ii-1]
snx[ii]=snx[ii-1]
plt.plot(tcl,snr,'.')
plt.plot(tcl,snx)
io=np.where(snx==snr)
plt.plot(tcl[io],snr[io],'o')
plt.ylim(0,10);
tcl=E[0,:].T
clx=E[1,:].T
snr=E[2,:].T
np.shape(E)
F=np.zeros((190,10))
F[:,0]=tcl
F[:,1]=clx
F[:,2]=snr
F[1:,3]=tcl[1:]-tcl[:-1]
ncl=np.shape(F)[0]
idet=np.array(io).T
#idet = np.array(np.where((snr>2) & (clx>500))).T
print(np.shape(idet))
print(ncl)
#idet=(0,3,9,11,13,15,19)
F[idet,4]=1
for ii in range(1,ncl):
if F[ii-1,4]==1:
F[ii,5]= F[ii,3]
else:
F[ii,5]= F[ii-1,5]+F[ii,3]
for ii in range(1,ncl):
if F[ii,4]==1: F[ii,6]= F[ii,5]
print(np.shape(F[idet,:]))
print(np.array_str(np.squeeze(F[idet,:6]), precision=4, suppress_small=True))
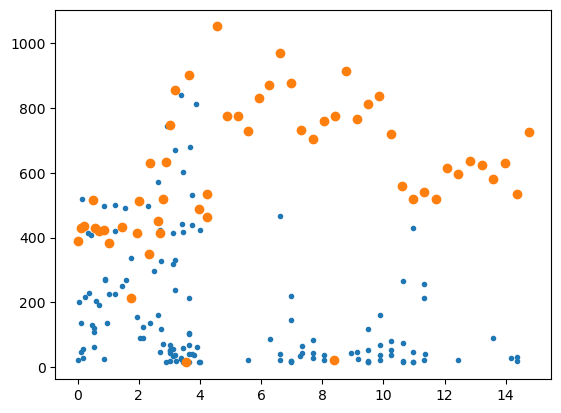
plt.plot(F[:,0],F[:,1:2],'.')
plt.plot(F[idet,0],F[idet,1],'o')
#plt.xlim(0,2)
plt.show()
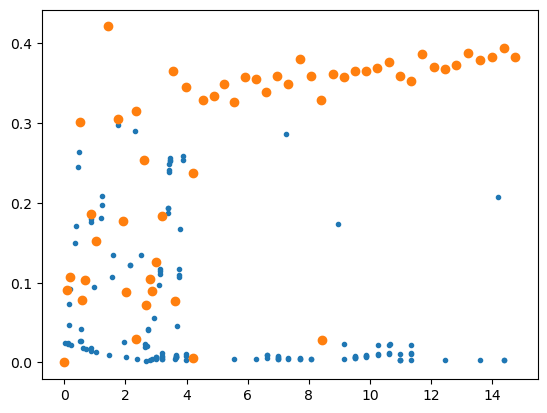
plt.plot(F[:,0],F[:,5],'.');
plt.plot(F[idet,0],F[idet,6],'o');
#plt.ylim(0,0.5);
#plt.xlim(0,2);
(55, 1)
190
(55, 1, 10)
[[ 0.0063 389. 3.3482 0. 1. 0. ]
[ 0.0974 429. 3.4317 0.0664 1. 0.0911]
[ 0.2048 435. 3.4353 0.015 1. 0.1074]
[ 0.5062 516. 2.8786 0.0374 1. 0.3014]
[ 0.5848 430. 3.4163 0.0368 1. 0.0786]
[ 0.688 420. 3.4984 0.0853 1. 0.1032]
[ 0.8736 423. 4.0005 0.0061 1. 0.1857]
[ 1.026 384. 4.0226 0.0581 1. 0.1524]
[ 1.4472 434. 3.9339 0.2124 1. 0.4212]
[ 1.752 213. 2.4612 0.0077 1. 0.3048]
[ 1.9296 414. 3.0561 0.1776 1. 0.1776]
[ 2.0183 512. 4.2049 0.0625 1. 0.0887]
[ 2.3331 350. 2.4923 0.0242 1. 0.3148]
[ 2.363 631. 4.5123 0.0299 1. 0.0299]
[ 2.6165 451. 4.7759 0.1184 1. 0.2535]
[ 2.6881 415. 5.0102 0.0489 1. 0.0717]
[ 2.7924 520. 5.4576 0.0617 1. 0.1043]
[ 2.8821 632. 6.1829 0.0868 1. 0.0897]
[ 3.0074 747. 6.3264 0.0691 1. 0.1254]
[ 3.1905 855. 7.0151 0.066 1. 0.183 ]
[ 3.5562 18. 1.0011 0.1099 1. 0.3657]
[ 3.6331 901. 7.0676 0.0769 1. 0.0769]
[ 3.9781 489. 3.7122 0.0864 1. 0.345 ]
[ 4.2159 533. 3.8015 0.2268 1. 0.2378]
[ 4.2215 465. 3.9447 0.0055 1. 0.0055]
[ 4.5501 1051. 4.4507 0.3286 1. 0.3286]
[ 4.8837 776. 5.2476 0.3336 1. 0.3336]
[ 5.2328 775. 5.2481 0.3491 1. 0.3491]
[ 5.5596 730. 5.6525 0.3268 1. 0.3268]
[ 5.9171 830. 5.1444 0.3535 1. 0.3576]
[ 6.2721 872. 6.3701 0.355 1. 0.355 ]
[ 6.6109 970. 6.9574 0.334 1. 0.3388]
[ 6.9701 878. 6.9528 0.3494 1. 0.3592]
[ 7.3189 731. 6.1041 0.0623 1. 0.3487]
[ 7.6995 703. 6.283 0.3755 1. 0.3806]
[ 8.0582 760. 5.557 0.3534 1. 0.3587]
[ 8.3869 23. 0.916 0.3242 1. 0.3287]
[ 8.4156 775. 5.551 0.0286 1. 0.0286]
[ 8.7768 914. 5.2381 0.3612 1. 0.3612]
[ 9.1348 766. 4.9692 0.1844 1. 0.358 ]
[ 9.5005 813. 5.3372 0.342 1. 0.3657]
[ 9.8658 837. 5.8132 0.3576 1. 0.3653]
[ 10.2355 720. 5.1118 0.3606 1. 0.3696]
[ 10.6127 558. 4.9004 0.3554 1. 0.3772]
[ 10.9713 520. 5.2808 0.3354 1. 0.3586]
[ 11.3241 542. 5.0275 0.3424 1. 0.3529]
[ 11.7109 519. 4.3604 0.3644 1. 0.3868]
[ 12.0814 616. 4.4328 0.3705 1. 0.3705]
[ 12.4491 595. 4.3545 0.3677 1. 0.3677]
[ 12.8222 636. 4.3863 0.3696 1. 0.373 ]
[ 13.2103 625. 4.4312 0.3881 1. 0.3881]
[ 13.5891 582. 4.5151 0.3788 1. 0.3788]
[ 13.9718 630. 4.5575 0.3795 1. 0.3827]
[ 14.3654 535. 4.8423 0.186 1. 0.3936]
[ 14.7477 726. 4.7928 0.3789 1. 0.3823]]
# modified after https://www.askpython.com/python/examples/k-means-clustering-from-scratch
#Importing required modules
import numpy as np
from scipy.spatial.distance import cdist
n1=np.where(E[0,:]<2)[0]
t=E[0,n1].T
x=E[1:,n1].T
k=5
nit=10
# initialize labels
nd=np.shape(x)[0]
labels = np.mod(range(nd),k)
centroids = x[[range(k)][0], :]
variances = 0*centroids
def mCluster(x,labels,k,centroids,variances):
for ii in range(k):
ni=labels==ii
if np.sum(ni)>0:
tmp=x[ni]
m1= tmp.mean(axis=0)
m2= (tmp*tmp).mean(axis=0)
else:
m1=0
m2=0
centroids[ii,:]=m1 # centroid
variances[ii,:]=m2-m1**2 # variance
return centroids,variances
centroids,variances=mCluster(x,labels,k,centroids,variances)
print(labels,variances.trace())
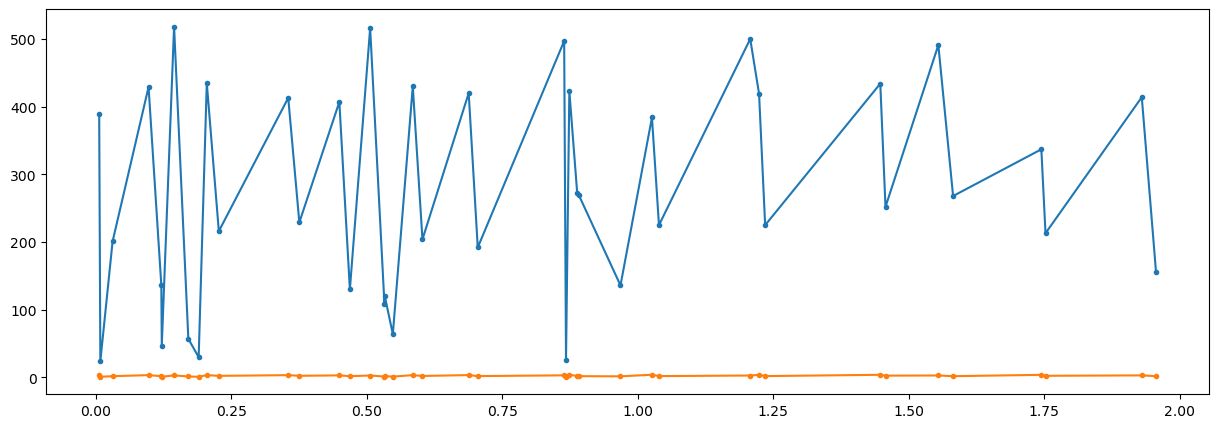
fig = plt.figure("figure.figsize",[15,5])
plt.plot(t,x,'.-')
plt.show()
#Repeating the above steps for a defined number of iterations
best=np.Inf
for ni in range(nit):
#Updating Centroids by taking mean of Cluster it belongs to
centroids,variances=mCluster(x,labels,k,centroids,variances)
##
# if variance get worth break loop
inert=variances.trace()
if inert >= best: break
best=inert
#
distances = cdist(x, centroids ,'euclidean')
labels = np.array([np.argmin(ii) for ii in distances])
for ii in range(k):
ni=np.where(labels==ii)
if len(ni)>0:
tcl=tt[ni]
if len(ni)>1:
ici=tcl[1:]-tcl[:-1]
print(ni,labels,best,np.shape(centroids))
for idat in range(nc-1):
fig = plt.figure("figure.figsize",[15,5])
u_labels = np.unique(labels)
for label in u_labels:
plt.plot(t[labels == label] , x[labels == label,idat],'.-', label = label)
plt.legend()
plt.show()
[0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1
2 3 4 0 1] 18988.49102369028
(array([26], dtype=int64),) [1 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2 2 2 1 2 1 2 1 2 1 4 3 2 1 2 1 1 2 1 3 1
3 1 2 1 2] 18988.49102369028 (5, 2)
(array([26, 27, 38], dtype=int64),) [1 0 3 1 2 0 1 0 0 1 3 1 3 1 2 1 2 2 0 1 3 1 2 1 0 1 4 4 2 1 3 1 1 3 1 3 1
3 4 3 1 2] 0.1487966343315108 (5, 2)
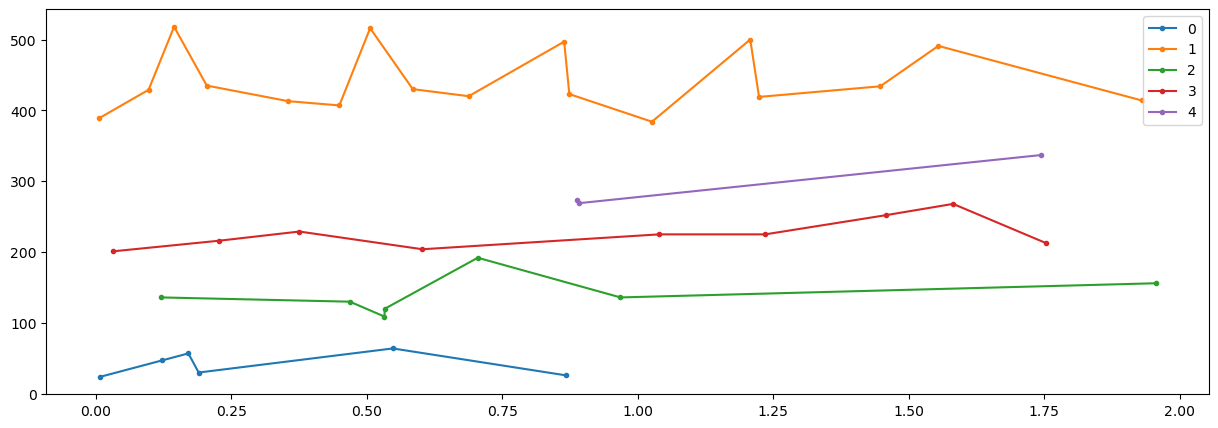
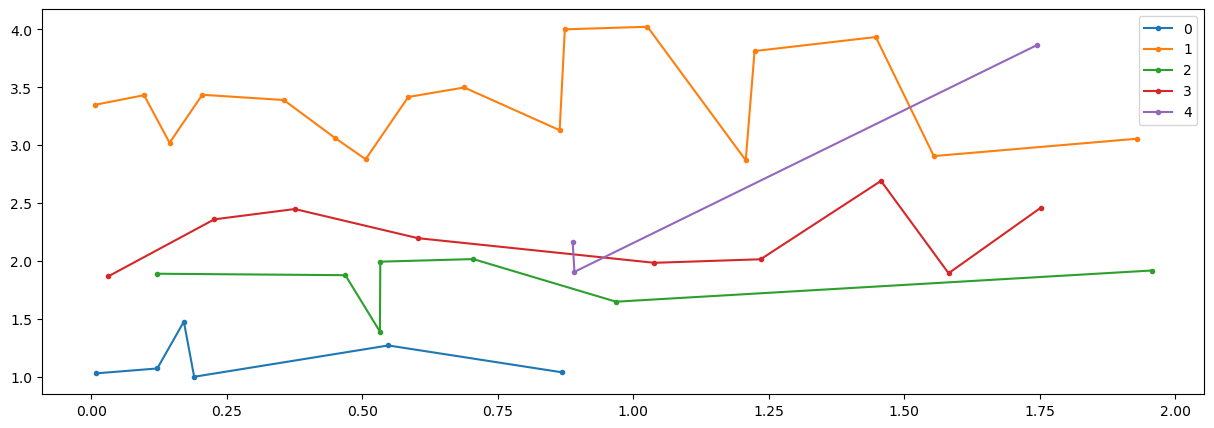
def doClickTrain(inp,tcl,pcl,icm,cmin):
# inp:
# tcl: click time
# pcl: click power
# icm:
# cmin: min clik interval (e.g. 0.15)
K=len(icm);
#
in0=0*icm;
in1=0*icm;
in2=0*icm;
#=============================================================
for nn in range(10):
count=0;
#
for ii in range(1,len(tcl)):
# if we have a free click
if inp[ii,10]==0:
dd1k=np.inf+0*icm;
dd2k=np.inf+0*icm;
ij=len(tcl);
for kk in range(K):
# find next click
for jj in range(ii+1,len(tcl)):
if abs(inp(jj,1))==1+2*(kk-1):
ij=jj;
break
# check if still space for new click in kk
if in0[kk]>0:
if tcl[ij]-tcl[in0[kk]]<1.5:
continue
#
if in2[kk]>0:
icin=tcl[in0[kk]]-tcl[in1[kk]];
if icin<0: icin=1/3;
ddkx=np.abs(tcl[ii]-tcl[in2[kk]]-3*(icin));
if ddkx<dd1k[kk]: dd1k[kk]=ddkx;
if dd1k[kk]>cmin and in1[kk]>0:
icin=tcl[in0[kk]]-tcl[in1[kk]];
if icin<0: icin=1/2;
ddkx=np.abs(tcl[ii]-tcl[in1[kk]]-2*(icin));
if ddkx<dd1k[kk]: dd1k[kk]=ddkx;
if dd1k[kk]>cmin and in0[kk]>0:
icin=1;
ddkx=np.abs(tcl[ii]-tcl[in0[kk]]-icin);
if ddkx<dd1k(kk): dd1k[kk]=ddkx;
if in1[kk]>0:
dpcl=pcl[in0[kk]]-pcl[in1[kk]];
dd2k[kk]=np.abs(pcl[ii]-pcl[in1[kk]]-2*dpcl);
elif in0[kk]>0:
dd2k[kk]=abs(pcl[ii]-pcl[in0[kk]]);
# do we have a best allocation?
[d1x,k1x]=np.min(dd1k);
[d2x,k2x]=np.min(dd2k);
if k1x==k2x: #have same best allocation
kx=k1x;
if d1x<cmin: #have a good click
inp[ii,:]=[1+2*(kx-1),ii,0];
count=count+1;
# else: # have conflicting allocations
# for the moment skip
# [d1x k1x,d2x,k2x pcl(ii) pcl(in0(kk))]
if np.mod(np.abs(inp(ii,1))-1,2) ==0: # have marked click
kx=1+np.floor((np.abs(inp(ii,1))-1)/2);
in2[kx]=in1[kx]; # so shift all back
in1[kx]=in0[kx];
in0[kx]=ii;
if count==0:
break
return inp