BLM_2: Wave propagation

BLM_2: Wave propagation#

Waves are the consequence of forcefully displacing some particles (gas/water/atoms) from the equilibrium state. the resulting propagating wave is mathematically described by the wave equation.

Equation of motion of forcefully displaced particles#

To derive the wave equation one needs three different physical laws and equations.

Newton’ law of motion:#

Newton: “a change in motion is proportional to the motive force impressed and takes place along a stright line in which the force is impressed”

In mathematical terms

(219)#\[\begin{equation} m\frac{d}{dt}(u)=F_u \end{equation}\]

where \(m\) is the particle mass that is considered constant and \(u\) is the velocity of the particles

Restoring force of pressure gradient:#

If a (spherical) particle volume is forefully changed by external pressure then the restoring force is proportional to the radial pressure variation

(220)#\[\begin{equation} F_p = - \frac{d}{dr} P \end{equation}\]

where \(V=m\rho\) is the (spherical) volume of the particles and \(r\) is measured along the radial dimension of the spherical volume.

Equation of continuity:#

Relative changes in particle densities is compensated by a velocity gradient and for spherical symetric motion (pulsing sphere) we get

(221)#\[\begin{equation} \frac{1}{\rho}\frac{d}{dt}\rho + \frac{d}{dr}u = 0 \end{equation}\]

Wave equation#

Combining all three equations one can obtain the wave equation that is the mathematical description of propagating waves and disturbances

(222)#\[\begin{equation} \frac{d^2(rP)}{dt^2} = c^2\frac{d^2(rP)}{dr^2} \end{equation}\]

The solution of this equation is any function of the form

(223)#\[\begin{equation} rP = f(ct \pm r) \end{equation}\]

This can easily be verified by the second derivatives with respect to time \(t\) and range \(r\). The form of the solution \(f(ct \pm r)\) is an indication that the time evolution of waves is directly related with spatial distribution of the waves.

Direction of propagation#

The solution to the spherical wave equation contains as argument \((ct \pm r)\) which means that for any solution we have two cases

  • \((ct - r)\) that is, for increasing time \(t\) the range \(r\) is increasing (wave is outgoing, diverging from origin)

  • \((ct + r)\) that is, for increasing time \(t\) the range \(r\) is decreasing (wave is incomming, converging to origin)

Example: Gaussian pulse#

Define a Pulse

(224)#\[\begin{equation} f(ct-r)=A(ct-r)\cos(k(ct-r)) \end{equation}\]

where the amplitude function \(A(ct-k)\) is given by a Gaussian shape

(225)#\[\begin{equation} A(ct-r)=P_0\exp{\Big(-\frac{1}{2}\big(\frac{ct-r}{\sigma}\big)^2\Big)} \end{equation}\]

and the “wavenumber” \(k\) is defined as

(226)#\[\begin{equation} k=\frac{2\pi}{\lambda} \end{equation}\]

and therefore

(227)#\[\begin{equation} P(t,r)=\frac{P_0}{r}\exp{\Big(-\frac{1}{2}\big(\frac{ct-r}{\sigma}\big)^2\Big)}\cos\big(\frac{2\pi}{\lambda}(ct-r)\big) \end{equation}\]

In the following examples we consider two cases observing a acoustic wave

  • time snap shot after 10 ms

  • time series at 15 m distance from origin

import numpy as np
import matplotlib.pyplot as plt
#
c=1500   # m/s
Po=1
sigma=1 # m
lam=3  # m

def Pulse(c,t,r,sigma,lam):
    return 1/r*np.exp(-1/2*((c*t-r)/sigma)**2)*np.cos(2*np.pi/lam*(c*t-r))

#=== case 1 ===  
r=np.arange(0.1,35,0.1)   # m
t=0.01                    # s time of snaphot
x1=Po*Pulse(c,t,r,sigma,lam)
print(np.shape(r),np.shape(x1))
#
plt.plot(r,x1)
plt.xlabel("Range [m]")
plt.show()

#=== case 2 ===
r=15                        # m fixed distance
t=np.arange(0,0.02,0.1e-3); # s
x2=Po*Pulse(c,t,r,sigma,lam)
print(np.shape(t),np.shape(x2))
#
plt.plot(t*1000,x2)
plt.xlabel("Time [ms]")
plt.show()

(349,) (349,)
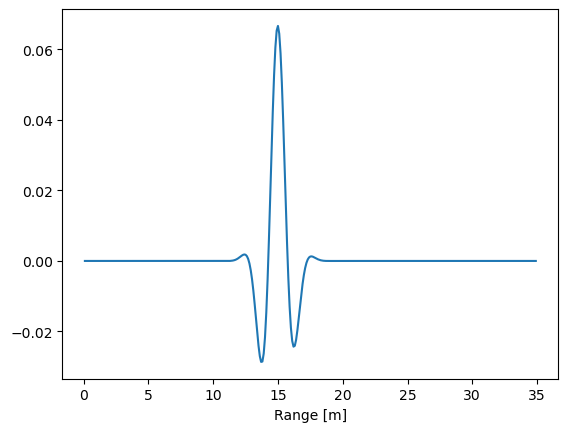
../_images/8f10b4f2b72b3e1107433445c340ae7aff8029818f185642b43bbfe806add9f0.png 
(200,) (200,)
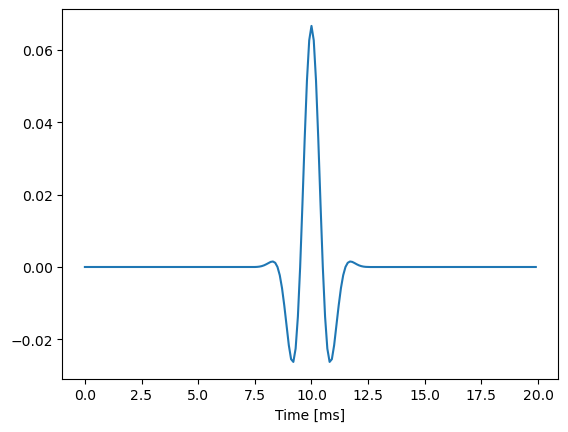
../_images/276a86c40bc385c7ea79da6f86816a487cfc4c09e292eda3234a2a6efa5f53f2.png

Observations#

The resulting measurements (case 1) and (case 2) show more or less the same wave form. Only difference is that the time snap shot, which measures the wave at different ranges is effected by the attenutation due to geometric speading, while measurements at a fixed range will experience always the same attenuation.

Contents